Pada Buku Matematika kelas 12 terdapat Contoh Soal 4.1, jawaban dari soal tersebut akan dibahas di bawah ini, namun sebaiknya siswa tidak menjadikan artikel ini sebagai acuan. Siswa lebih baik mencoba menjawab sendiri sebelum melihat jawaban ini.
Kunci jawaban soal Matematika kelas 12 halaman 190 dan 191 semester 2 Contoh Soal 4.1
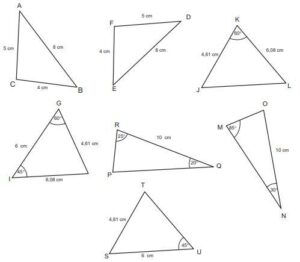
1. Identifikasi segitiga-segitiga berikut yang kongruen menggunakan aturan sinus dan kosinus.
Pembahasan:
Segitiga ABC kongruen dengan segitiga DEF (konjektur sisi-sisi-sisi).
Perhatikan segitiga MON. Besar sudut MON = 180° – (85° + 20°) = 75°.
Diperoleh segitiga PRQ kongruen dengan segitiga MON karena sudut PRQ = sudut MON, RQ = ON, sudut RQP = sudut ONM (konjektur sudut-sisi-sudut).
Perhatikan segitiga GHI, besar sudut GHI = 180° – (45° + 69°) = 66°.
Diperoleh segitiga GHI kongruen dengan segitiga JKL karena GH = JKm sudut GHI = sudut JKL, HI = KL (Konjektur sisi-sudut-sisi).
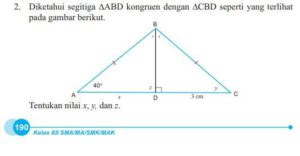
2. Diketahui segitiga ∆ABD kongruen dengan ∆CBD seperti yang terlihat pada gambar berikut. Tentukan nilai x, y, dan z.
Pembahasan:
Karena segitiga ∆ABD kongruen dengan ∆CBD, berarti sisi-sisi dan sudut-sudut yang bersesuaian sama besar. Sehingga AD = CD, ∠BAD
= ∠BCD, dan ∠BDA = ∠BDC.
Dengan demikian, x = 3 cm, y = 40°, z = 90°.
3. Diketahui segitiga ABC dengan A(-2, 6), B(4, 12), dan C(10,6 ; 9,2).
a. Tentukan banyangan segitiga ABC jika dirotasi dengan pusat O(0,0) sebesar 60° berlawanan arah jarum jam
Pembahasan:
Misalkan titik-titik A’, B’, dan C’ secara berturut-turut adalah bayangan titik-titik A, B, C karena rotasi dengan O(0,0) sebesar 60° berlawanan arah jarum jam. Diperoleh koordinat titik-titik A’, B’, dan C’ adalah

b. Gambarkan segitiga ABC dan bayangannya dalam 1 bidang koordinat Cartesius.
Pembahasan:
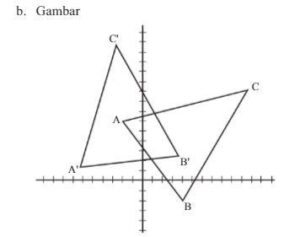
c. Jelaskan apakah segitiga ABC dan bayangannya merupakan dua segitiga yang sebangun
Pembahasan:
Karena transformasi rotasi mengawetkan jarak, diperoleh AB=A’B’, AC= A’C’, BC=B’C’. Jadi segitiga ABC dan segitiga bayangannya merupakan segitiga-segitiga sebangun dan juga segitiga-segitiga kongruen.
d. Tentukan perbandingan luas segitiga ABC dengan luas segitiga bayangannya.
Pembahasan:
Karena segitiga ABC kongruen dengan segitiga bayangannya maka perbandingan luas daerah kedua segitiga tersebut adalah 1:1.
4. Diketahui segitiga ABC dengan A(3,0), B(6,2), dan C(6,4).
a. Tentukan bayangan segitiga ABC oleh dilatasi dengan pusat O(0,0) dan faktor skala 3.
Pembahasan:
Misalkan titik-titik A’, B’, dan C’ secara berturut-turut adalah bayangan titik-titik, A, B, C karena dilatasi dengan pusat O(0,0) dan factor skala 3. Diperoleh koordinat titik-titik A’, B’, dan C’ adalah
b. Gambarkan segitiga ABC dan bayangannya dalam 1 bidang koordinat Cartesius.
Pembahasan:
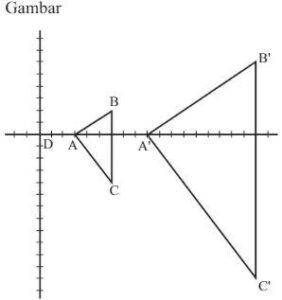
c. Jelaskan apakah segitiga ABC dan bayangannya merupakan dua segitiga yang sebangun.
Pembahasan:
Segitiga ABC dan bayangannya merupakan dua segitiga yang sebangun karena AB/A’B’ = BC/B’C’ = AC/A’C’ = 1/3.
d. Tentukan perbandingan luas segitiga ABC dengan luas segitiga bayangannya.
Pembahasan:
Perbandingan luas daerah segitiga ABC dengan luas daerah segitiga A’ B’ C’ adalah 1:9.
5. ABDF adalah persegi dan BC = EF. Tentukan pasangan segitiga-segitiga yang kongruen pada gambar berikut.
Pembahasan:
Segitiga ABC kongruen dengan segitiga AFE karena AB = AF, BC = FE, dan sudut ABC = sudut AFE = 90°.
Segitiga AGC kongruen dengan segitiga AGE karena AC = AE, GC = GE, dan AG = AG.
Itulah tadi pembasan mengenai Kunci Jawaban Matematika Kelas 12 Semester 2 Halaman 190 dan 191. Semoga bemanfaat.

