Soal Dan Kunci Jawaban Matematika Kelas 8 Halaman 10

Oleh Diposting pada

Ayo Kita Menalar

Diketahui persegi panjang ABCD. Terdapat titik Q di luar persegi panjang.

Bagaimanakah cara kalian dalam menentukan hubungan antara panjang AQ, BQ, CQ, dan DQ?

Untuk membantu kalian menentukan hubungan keempat panjang ruas garis tersebut, perhatikan Gambar 6.7 di samping. (Gambar bisa bermacam-macam).

 

 

Jawaban:

Ikuti langkah-langkah berikut:

  • Buat garis yang sejajar dengan garis AB dan melalui Q.
  • Buat garis dari perpanjangan AD sehingga memotong garis yang telah dibuat pada langkah i.
  • Buat garis dari perpanjangan BC sehingga memotong garis yang telah dibuat pada langkah i.
  • Buat garis yang sejajar dengan AD dan BC melalui Q.
  • Beri nama pada setiap ruas garis sehingga membentuk gambar seperti di bawah ini.

 

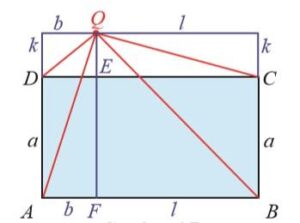
Perhatikan ∆AFQ. Berlaku teorema Pythagoras.

AQ² = AF² + FQ²
AQ² = b² + (a + k)² …………………. (1)

 

Perhatikan ∆DEQ. Berlaku teorema Pythagoras.

DQ² = DE² + EQ²
AQ² = b² + k² …………………. (2)

 

Perhatikan ∆FBQ. Berlaku teorema Pythagoras.

BQ² = FQ² + FB²
BQ² = (a + k)² + l² …………………. (3)

Perhatikan ∆CEQ. Berlaku teorema Pythagoras.

CQ² = CE² + EQ²
CQ² = l² + k² …………………. (4)

Dari persamaan (1), (2), (3), dan (4) dapat diperoleh bahwa AQ² + CQ² = DQ² + BQ²

 

Jadi, hubungan antara panjang AQ, BQ, CQ, dan DQ adalah AQ² + CQ² = DQ² + BQ².

 

 

Disclaimer : Latihan soal dan jawaban ini bukan bocoran penilaian harian. Ini hanya sebagai referensi belajar bagi siswa. Jika ada kesamaan soal maka itu hanya kebetulan saja.

Posting terkait:

Rekomendasi:

Gambar Gravatar
Cindy Monica - https://cytricks.com
Hi, Perkenalkan nama saya Cindy Monica, pemilik dari situs cytricks.com. Memiliki kegemaran terhadap dunia menulis, internet, dan bisnis, menjadikan saya tergerak untuk membuat situs ini sebagai media informasi terhadap pembaca.

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *